Hàm số bậc nhất là chuyên đề toán học quan trọng trong chương trình đại số của cấp bậc trung học cơ sở.chúng ta cùng tìm hiểu xem giũa hàm số bậc nhất lớp 9 và hàm số bậc nhất lớp 10 có gì khác biệt, tính chất đồ thị hàm số, công thức và cách giải quyết các bài tập như thế nào cho chính xác nhất.
Lý thuyết về hàm số bậc nhất :
Định nghĩa hàm số bậc nhất
– Hàm số bậc nhất là hàm được cho bởi công thức y = ax + b trong đó a, b là những số cho trước và a ≠ 0.
– Như vậy công thức hàm số bậc nhất là : y = ax + b
Ví dụ : hàm số bậc nhất: y = 8x + 4b, y = 3x , y = -5x – 1, y = (1/2)x + 7…
Tính chất của hàm số bậc nhất :
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
- Đồng biến trên R khi a > 0
Hàm số y = f(x) gọi là đồng biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x1 < x2 thì f(x1 ) < f(x2 ) - Nghịch biến trên R khi a < 0.
Hàm số y = f(x) gọi là nghịch biến trong khoảng nào đó nếu với mọi x1 và x2 trong khoảng đó sao cho x1 < x2 thì f(x1 ) > f(x2 )
Bảng biến thiên:
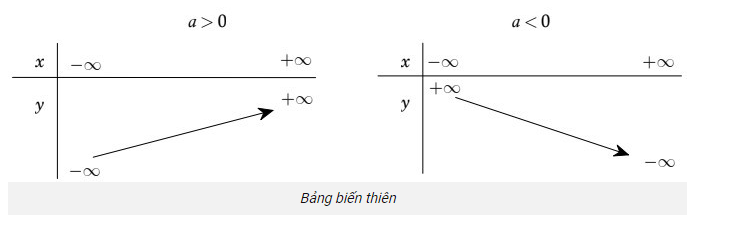
CÁCH VẼ ĐỒ THỊ HÀM SỐ BẬC NHẤT Y = AX + B
Trường hợp 1: Khi b=0
Khi b = 0 thì y =ax là đường thẳng di qua gốc tọa độ O(0;0) và điểm A (1;a) đã biết
Xét trường hợp y= ax với a khác 0 và b khác 0
Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng, do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó
- Cách thứ nhất:
Xác định hai điểm bất kỳ của đồ thị , chẳng hạn:
Cho x = 1 tính được y = a + b, ta có điểm A ( 1; a+b)
Cho x = -1 tính được y = -a + b, ta có điểm B (-1 ; -a + b) - Cách thứ hai:
Xác định giao điểm của đồ thị với hai trục tọa dộ:
Cho x = 0 tính được y = b, ta được điểm C (-b/a;0)
Cho y = 0 tính được x = -b/ a, ta có điểm D (-b/a; 0)
Vẽ đường thẳng qua A, B hoặc C, D ta được đồ thị của hàm số y = ax + b
Dạng đồ thị của hàm số y = ax + b ( a khác 0)
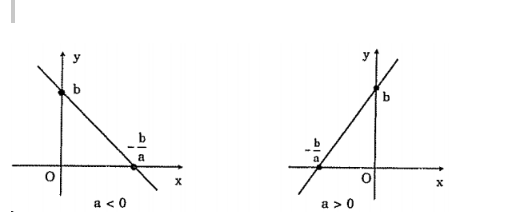
Trường hợp 2: Khi b khác 0
Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.
- Bước 1: Cho x=0=>y=b. Ta được điểm P(0;b)∈Oy.
Cho y=0=>x=−ba. Ta được Q(−ba;0)∈0x. - Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y=ax+b.
Ví dụ :
Bài 1 :
Chứng minh ba đường thẳng đồng quy, ba điểm thẳng hàng
Ví dụ: Cho ba điểm A(0;3),B(−1;1),C(1;5)
– Viết phương trình đường thẳng AB
– CMR: A, B, C thẳng hàng
Cách giải:
1.Gọi phương trình đường thẳng AB có dạng: y=ax+b
Ta có:
A(0;3)∈(AB)⇒3=a.0+b
B(−1;1)∈(AB)⇒1=a.(−1)+b
Suy ra (AB):y=2x+3
2. Xét xem điểm C(1;5) có thuộc (AB) hay không
Thay điểm C(1;5) vào phương trình (AB):y=2x+3
Ta có: 5=2.1+3 (luôn đúng)
Suy ra A, B, C thẳng hàng.
Bài 2
Vẽ đồ thị hàm số của các hàm số
a, y= 2x
b, y=-3x+3
Lời giải:
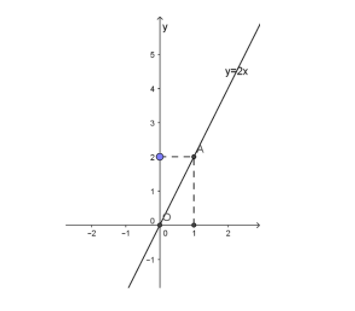
a, y=2x
Đồ thị hàm số y=2x đi qua điểm O(0; 0) và điểm A(1; 2)
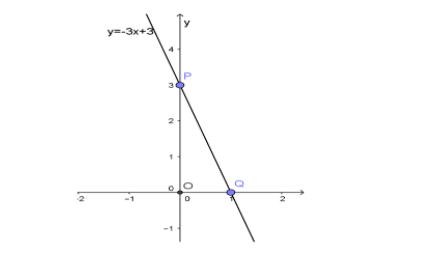
b, y=-3x+3
Cho x=0 thì y=3, ta được điểm P(0; 3) thuộc trục tung Oy
Cho y=0 thì x=1, ta được điểm Q(1; 0) thuộc trục hoành Ox
Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y=-3x+3
Bài 3
Cho đường thẳng y=(k+1)x+k. (1)
a, Tìm giá trị của k để đường thẳng (1) đi qua gốc tọa độ.
b, Tìm giá trị của k để đường thẳng (1) cắt trục tung tại điểm có tung độ bằng 2.
c, Tìm giá trị của k để đường thẳng (1) song song với đường thẳng y=5x-5.
Gọi ý lời giải :
a, Đường thẳng y=ax+b đi qua gốc tọa độ khi b=0, nên đường thẳng y=(k+1)x+k qua gốc tọa độ khi k=0, khi đó hàm số là y=x.
b, Đường thẳng y=ax+b cắt trục tung tại điểm có tung độ bằng b. Do đó, đường thẳng y=(k+1)x+k cắt trục tung tại điểm có tung độ bằng 2 khi k=2.
Vậy k=2 và đường thẳng cần tìm là y=3x+2
c, Đường thẳng y=(k+1)x+k song song với đường thẳng y=5x-5 khi và chỉ khi k+1=5 và. Từ đó suy ra k=4.
Vậy hàm số cần tìm là y=5x+4.
Trên đây là những kiến thức cơ bản về tính chất,công thức và định nghĩa thế nào là hàm số bậc nhất.Cách vẽ đồ thị cũng như bảng biến thiên của hàm số, Nhắc lại: hàm số bậc nhất là hàm số có dạng y = ax + b với a khác 0; hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0). Ở bài viết sau, các em sẽ được tìm hiểu về những dạng toán liên quan đến hàm số bậc nhất hay gặp và phương pháp giải.
xem thêm : Cách tính thể tích khối lăng trụ đứng, tam giác đều